Sediment Transport Model
FLOW-3D‘s Sediment Transport model can be used to evaluate scour and deposition, where three-dimensional flow components are driving the scouring process. FLOW-3D’s hydrodynamic model solves the full unsteady non-hydrostatic Reynolds-averaged Navier-Stokes equations that describe the flow physics. The hydrodynamic solver is fully coupled with a sediment transport module that simulates bedload and suspended sediment transport, entrainment and erosion for non-cohesive soils (Wei et al., 2014). All empirical relationships used in bedload, entrainment and settling processes are fully customizable, and up to 10 different sediment species (with different properties such as grain size, mass density and critical shear stress) can be defined. FLOW-3D is ideal for simulating local scour over short episodic time scales.
Modeling Capabilities
- Unsteady 3D mobile bed modeling
- Bedload and suspended sediment transport
- Non-cohesive sediment
- 10 individual grain size fractions
- Suspended sediment settling and entrainment
- Critical angle of repose
Applications
- River and coastal morphodynamics
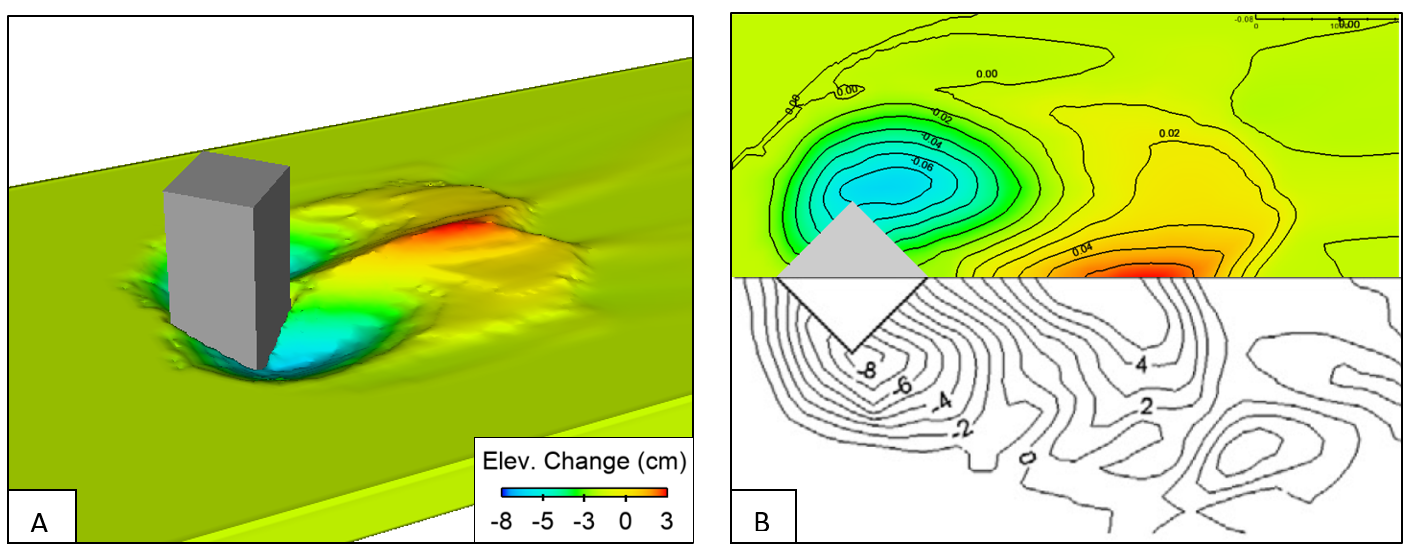
- Bridge pier and abutment scour
- Local scour at hydraulic structures
- Sedimentation basins
- Reservoir flushing
Sediment Transport Model
The Sediment Transport model was first introduced in version 8.0 (Brethour, 2009), and has gone through extensive revisions in version 11.1 (Wei et al., 2014), and most recently in version 12.0 (Flow Science, 2019). A schematic of the physical processes simulated in the numerical model is illustrated below.

In the numerical model, sediment can exist as packed bed and in a suspended state. A packed bed is an erodible solid object that is represented using the FAVOR™ technique for complex solid boundaries (Hirt and Sicilian, 1985). This is the same method used to represent solid objects in the hydrodynamic solver. The morphological change in the packed bed is governed by the conservation of sediment mass.
The morphological changes are governed by several different physical processes that are represented numerically in the model. These processes include bedload transport, entrainment and deposition. Bedload transport is the physical process of sediment moving laterally along the channel without being carried into suspension. Entrainment is the process by which turbulent eddies remove the grains from the top of the packed bed and transition to the suspended state. Packing is the process of grains settling out of suspension and depositing onto the packed bed. In the numerical model, this is the transition from the suspended to the packed bed state.
The relative rates of entrainment and packing control the exchange of sediment mass between the packed bed and suspended states. The model calculates bedload transport in each mesh cell containing the bed interface using the equation of Meyer-Peter Müller (1948), Nielsen (1992) or Van Rijn (1984). A sub-mesh method is employed to determine the amount of grains moving from the mesh cell into each mesh cell in its neighbor. The lifting velocity of grains in entrainment is calculated using the equation of Winterwerp et al. (1992). The settling velocity is calculated using Soulsby (1997). In the mesh cells containing the bed interface, location, orientation and area of the interface are calculated to determine the bed shear stress, dimensionless shear stress, bedload transport rates and entrainment rates. Bed shear stress in 3D turbulent flows is evaluated using the standard wall function with consideration of bed surface roughness that is proportional to the median grain size.
The suspended sediment is represented as a scalar mass concentration in the fluid. The concentration is assumed to be uniform in a given cell and is coupled with the fluid cell density and viscosity. For each species, the suspended sediment concentration is calculated by solving a transport equation.
Validations
The following five validation cases compare experimental data with simulation results from FLOW-3D’s Sediment Transport model.
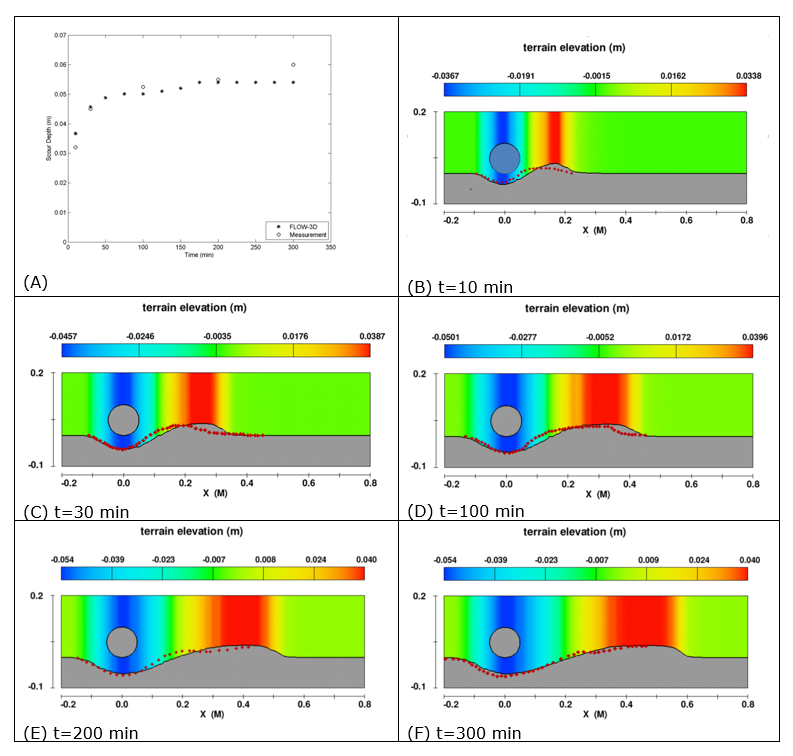
Mao (1986)
Experimental work was performed by Mao to obtain scour profiles of bed erosion underneath underwater horizontal pipelines. The plots below compare the results obtained using FLOW-3D with those from the experiments.
Plot A compares the maximum scour depth under the pipeline over time, while plots B through F overlay the scour profiles from the study, shown as red dots, with those from FLOW-3D.
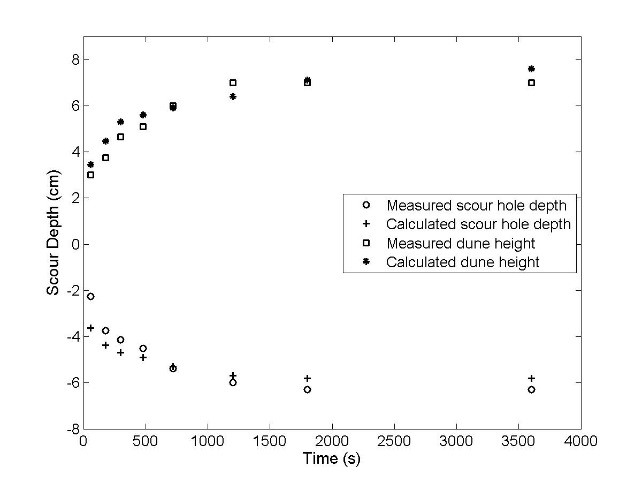
Chatterjee et al. (1994)
Experimental work was performed to obtain local scour profiles due to a submerged horizontal jet. The plot below compares the experimental versus FLOW-3D‘s numerical results for the scour hole depth and dune height as a function of time. The animation shows that the scour hole and dune height reach steady state in ~1 hour.
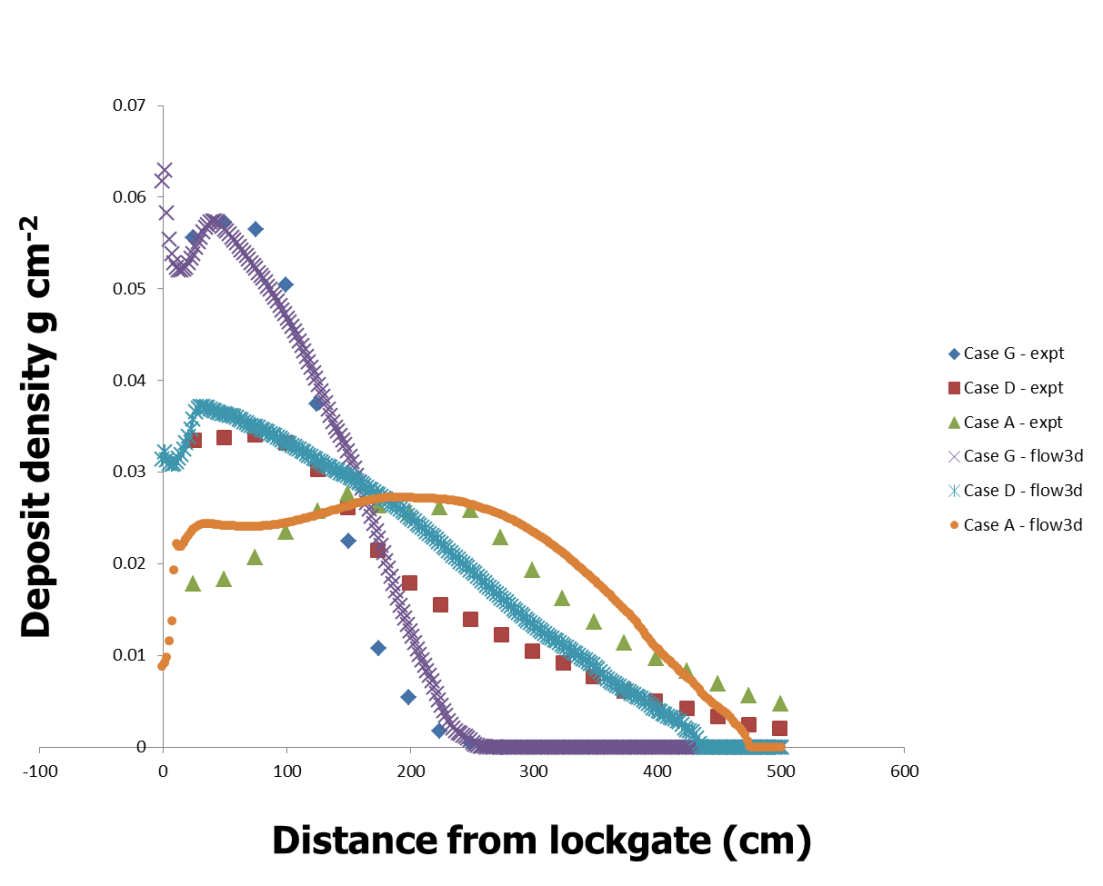
Gladstone et al. (1998)
In these experiments the propagation and deposition patterns of particle-laden flows were studied. The plot below compares experimental versus FLOW-3D simulation results from three different setups, labeled case A (100% 0.025mm size particles), case D (50% 0.069mm and 50% 0.025mm size particles), and case G (100% 0.069mm size particles).
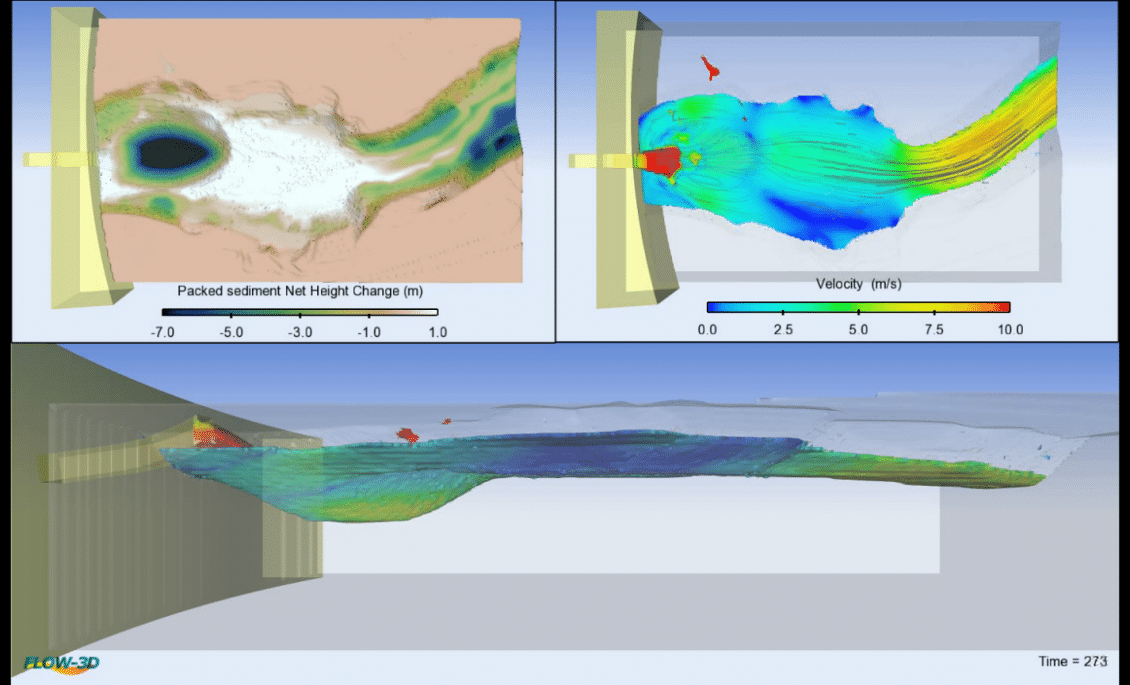
Faruque et al. (2006)
In this paper, the authors studied local scour by submerged three-dimensional wall jets via experiments. The table below compares the experimental versus FLOW-3D numerical results for 3D morphological changes in the scour hole for three different tailwater ratios.

References
- Brethour, J.M., Hirt, C.W., 2009, Drift Model for Two-Component Flows, FSI-14-TN-83, Flow Science, Inc.
- Chatterjee, S.S., Ghosh, S.N., and Chatterjee M., 1994, Local scour due to submerged horizontal jet, Journal of Hydraulic Engineering, 120(8), pp. 973-992.
- Faruque, M.A.A., Sarathi, P., and Balachandar R., 2006, Clear Water Local Scour by Submerged Three-Dimensional Wall Jets : Effect of Tailwater Depth, Journal of Hydraulic Engineering, 132(6), pp. 575-580.
- Flow Science, 2019, FLOW-3D Version 12.0 User Manual, Santa Fe, NM: Flow Science, Inc. https://www.flow3d.com
- Fox, B. and Feurich, R., 2019, CFD Analysis of Local Scour at Bridge Piers, Federal Interagency Sedimentation and Hydrologic Modeling Conference (SEDHYD), Reno, NV.
- Gladstone, C., Phillips, J.C., and Sparks R.S.J., 1998, Experiments on bidisperse, constant-volume gravity currents: propagation and sediment deposition, Sedimentology 45, pp. 833-843.
- Hirt, C.W. and Sicilian, J.M., 1985, A porosity technique for the definition of obstacles in rectangular cell meshes, 4th International Conference on Numerical Ship Hydrodynamics, Washington, D.C.
- Khosronejad, A., Kang, S., & Sotiropoulos, F., 2012. Experimental and computational investigation of local scour around bridge piers, Advances in Water Resources, 37, pp. 73-85.
- Mao, Y., 1986. The interaction between a pipeline and an erodible bed, PhD thesis, Institute of Hydrodynamics and Hydraulic Engineering, Technical University of Denmark, Lyngby, Denmark.
- Meyer-Peter, E. and Müller, R., 1948, Formulas for bed-load transport, Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research. pp. 39–64.
- Nielsen, P., 1992, Coastal bottom boundary layers and sediment transport (Vol. 4). World scientific.
- Soulsby, R., 1997, Dynamics of Marine Sands, Thomas Telford Publications, London.
- Van Rijn, L. C., 1984, Sediment Transport, Part I: Bed load transport, Journal of Hydraulic Engineering 110(10), pp. 1431-1456.
- Wei, G., Brethour, J.M., Grüenzner M., and Burnham, J., 2014, The Sediment Scour Model in FLOW-3D, Technical Note FSI-14-TN-99, Flow Science, Inc.
- Winterwerp, J.C., Bakker, W.T., Mastbergen, D.R. and Van Rossum, H., 1992, Hyperconcentrated sand-water mixture flows over erodible bed, Journal of Hydraulic Engineering, 118(11), pp. 1508–1525.