
Cavitation Model
What is Cavitation?
Cavitation is the rapid evolution of vapor and/or gas bubbles within fluid due to very low pressure in fluid flow, or due to a rise in temperature, which raises the saturation pressure. The sudden appearance (and subsequent collapse) of bubbles causes rapid changes in pressure within incompressible fluids, which in turn can cause severe mechanical damage.
Cavitation in HPDC
Additionally, cavitation can occur in high pressure die casting. The rapid movement of molten alloy through constrictions and curves in the die can result in rapid pressure drops and lead to subsequent cavitation. The resulting vapor bubbles can cause porosity in the final casting, or worse, cause damage to the die, contaminating the casting and leading to reduced die life. For these reasons, it is critical to understand where cavitation is likely to occur and its potential severity. Since initiating and visualizing cavitation through physical experimentation is difficult and potentially damaging, it is preferable to simulate the process.
Because of the high velocities and accompanying low pressures created in HPDC processes, cavitation is possible. Cavitation bubbles collapsing on the die surface can create pitting, which in turn causes surface quality issues on the casting as well as drastically shortening the life of expensive dies. FLOW-3D CAST’s cavitation potential model is a powerful tool for identifying areas on the die where cavitation is likely to occur.
Real-World Applications
- Simulate damaging cavitation within water and environmental structures
- Simulate cavitation during high pressure die casting that can cause die damage and casting porosity
- Simulate formation of thermal bubbles within MEMS devices
- Predict boiling behavior for heat transfer surfaces
- Predict mixing due to cavitation dynamics
Modeling Cavitation in FLOW-3D
FLOW-3D’s cavitation model has been successfully used to simulate thermal bubble jets and MEMS devices. FLOW-3D offers the option of “active” or “passive” models. The active model opens bubble regions while the passive model tracks and advects the presence of cavitation bubbles through the flow, but does not initiate the formation of bubble regions. The active model is best for cases where larger cavitation regions are expected and will affect the flow field, while the passive model is best for simulations where the brief appearance of small bubbles is expected. With the active model and calculation of energy transport, phase change is also an option; the bubble can further expand or contract due to evaporation or condensation at the interface.
Sample Results
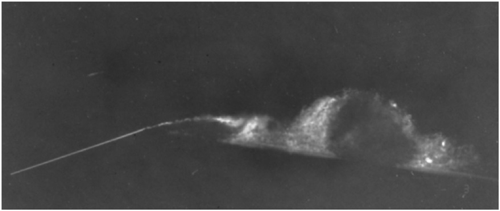
The animation below shows cavitation within a venturi with an entry velocity of 8m/s, a convergent slope of 18°, and a divergent slope of 8°. Again, the transient behavior of cavitation is well modeled, with the model predicting a cavitation cycle period of 17.4ms compared with the experimental result of 22ms (Stutz and Reboud 1997).
References
Lee, W., Hoopes, J.A., 1996, Prediction of Cavitation Damage for Spillways, Journal of Hydraulic Engineering, 122(9): 481-488.
Plesset, M.S., Prosperetti, A., 1977, Bubble Dynamics and Cavitation, Annual Revue of Fluid Mech, 9: 145-185.
Rouse, H., 1946. Elementary Mechanics of Fluids, New York: Dover Publications, Inc.
Stutz, B., Reboud, J.L., 1997, Experiments on unsteady cavitation, Experiments in Fluids, 22: 191-198.
