Granular Media
Many types of granular media are encountered in processing and manufacturing industries. Because of its unusual properties, granular material can often pose difficult problems for engineers seeking to transfer, mix or otherwise manipulate it for useful purposes. The granular media model is used to predict the behavior of a mixture of solid particles and a fluid that can be either gas or liquid, e.g., sand and air or sand and water. This mixture of granular solid and fluid is treated as an incompressible fluid that may be bounded by fee surfaces. The granular media model has been developed for flows of highly concentrated granular material. The model uses a “continuum” approach, that is, it is based on a continuous fluid representation of the sand, making no attempt to treat individual sand particles.
Modeling Granular Media
A mixture of sand and air, is a two-phase flow in which the air and sand materials flow with their individual velocities, but are coupled through momentum exchanges resulting from pressure and viscous stresses. In typical core sands the diameters of sand particles are on the order of tenths of millimeters and the volume fraction of the sand that is blown into a cavity is generally 50% or higher. In this range a strong coupling exists between the sand and air so their mixture can be modeled as a single, composite fluid. Two-phase effects resulting from differences in the velocities of the two materials are accounted for using an approximation for their relative velocity that is referred to as a Drift-Flux.
This composite flow with a relative velocity approach has been selected as the basis for the granular media model. It is assumed that the sand/air mixture can be represented as a single fluid with a sharp free surface at its boundary with the surrounding air. The composite fluid, however, is allowed to have a non-uniform density, depending on the degree of sand compaction. The viscosity of the mixture is a function of density and shear stress. Because the majority of momentum transfer is by particle-particle collisions the sand-air mixture has the character of a shear thickening material.
For the purpose of venting pure air regions in the cavity, they are treated as adiabatic bubbles. An adiabatic bubble is a region of air surrounded by fluid or solid walls. The pressure in a bubble is a function of the bubble volume and has a uniform value over the region occupied by the bubble. Vents allow air within bubbles to be vented to the exterior of the cavity.
Granular Media Applications
To illustrate some of the differences that can occur in a granular material as opposed to a fluid, a simple two-dimensional wedge shape hopper was set up with a 1 cm wide tube at the bottom. The simulation is started with the bottom tube empty.
Sand was initialized at its close packing limit of 0.63 volume fraction. Sand at the bottom of the opening to the discharge tube begins to fall under the action of gravity, but nearly all the sand above remains stationary, Figs. 1-4, where the color is the flow resistance caused by packing (red being perfectly rigid). In a short time a bubble-like region is formed and moves up toward the top surface of the sand. Only flow around the surface of the bubble is seen until the bubble reaches the top then it causes a collapse of the surface. The indentation in the top surface has localize flow that reduces its sides to a specified angle of repose of 34°. Meanwhile another bubble forms at the bottom to repeat this pattern.
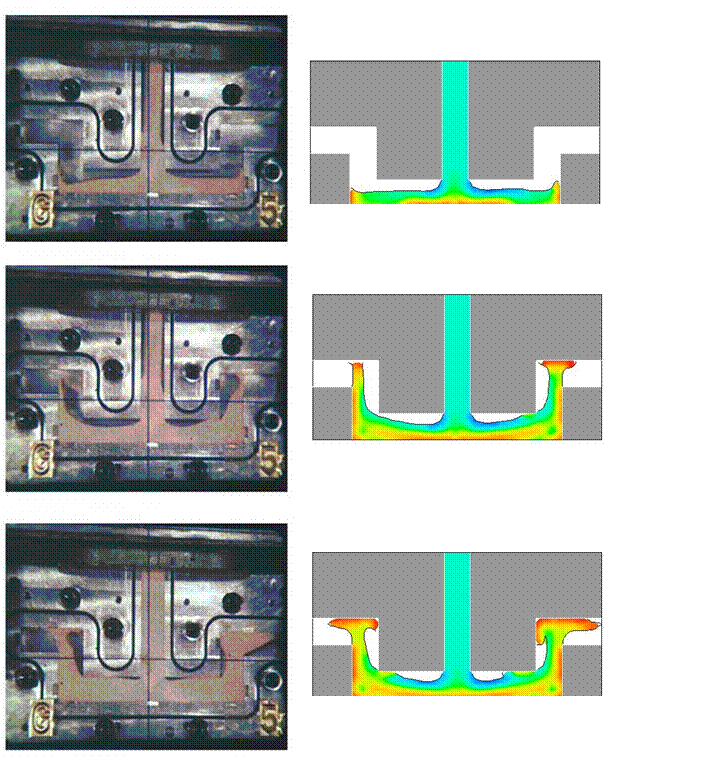
To illustrate the application of this new model, a simulation was performed to compare with data in the paper “Development and use of Simulation in the Design of Blown Cores and Moulds,” by D. Lefebvre, A. Mackenbrock, V. Vidal, V. Pavan and P.M. Haigh., Hommes & Fonderie, December 2004. The data is for a two-dimensional die geometry with one filling port. Venting of the die was asymmetric so that the influence of vents on the filling pattern could be studied.
The size of the simulation region was 30 cm wide by 15 cm high and 1 cm thick. Sand/air mixture of density 1.508 gm/cc was driven into the box with a pressure of 2 atmospheres absolute at the entrance to the box. There were five open vents on the right side of the box plus six more that were closed on the bottom and left side of the box. This arrangement leads to an asymmetric filling of the box.
The computational grid consisted of 80 mesh cells horizontally and 40 vertically. The time for the simulation to reach a fully filled core box was 0.07s and required a CPU time of about 8.9s running in serial mode on a 3.2GHz Pentium 4 PC computer (satisfyingly small, but of course, this was only a 2D case with 3200 cells in the computational region).
A comparison of the results from the continuum model simulation with photos from the Lefebvre, et al paper is given in Fig. 5. The visual agreement is seen to be very good in many details. The simulation captures the asymmetric influence of having vents closed on the left side.