Hydraulic Energy Losses
This article was contributed by Laurent Bilodeau, ing. Conception des aménagements de production Hydro-Québec Équipement.
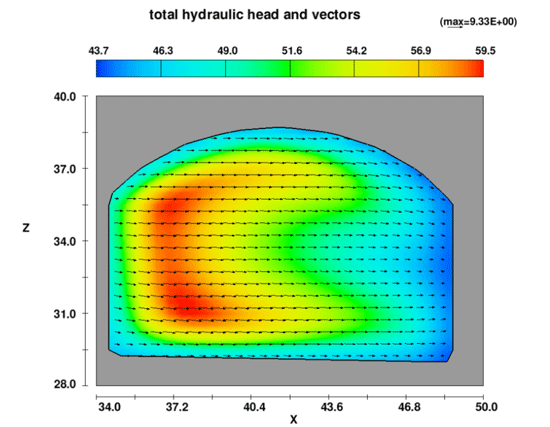
This note reviews the computation of hydraulic energy flow and total hydraulic head provided by FLOW-3D, with a particular interest for the evaluation of hydraulic energy dissipation rates. Our civil and environmental customers now use FLOW-3D HYDRO for these types of modeling and analysis. In FLOW-3D HYDRO, total hydraulic head was included among the variables that can be visualized directly from model outputs. Figure 1 shows the total hydraulic head distribution across a cut through a river diversion tunnel. In version 10, FLOW-3D HYDRO introduced hydraulic energy flow and total hydraulic head as integral values that can be computed with flux baffles, visualized as time series, and analyzed with external tools.
Total Hydraulic Energy
Bernoulli’s Equation
| e G | hydraulic energy density (J/m3 ) |
| p | pressure (Pa ≡ N/m2 ≡ J/m3 ) |
| g | gravity’s acceleration ( – 9,81 m/s2 ) |
| ρ | density (kg/m3 ) |
| u, v, w | velocity in x, y and z (m/s) |
| z | height (m) above some reference level, or altitude |
The Hydraulic Energy Simplified Cascade
Energy in general is considered to be a conservative quantity that transforms itself but is never lost. For the purposes of representing water flow in civil engineering, it is often sufficient to conceive of energy transformations as a cascade starting with gravitational potential energy, transforming into kinetic energy and then into heat energy. It is also conventional to further limit the scope of the energy cascade by modeling explicitly the quantities of only the first two forms (potential and kinetic).
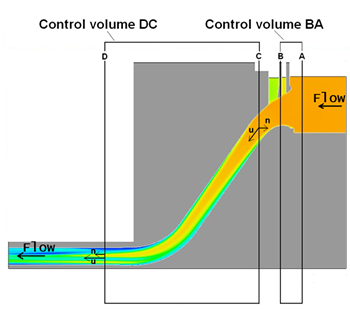
The hydraulic energy cascade is demonstrated well by the case of a flow plunging from a weir into a pool, as illustrated in Figure 2.
Following the track of a particle as indicated in the figure:
- At position A, a water particle sits almost motionless in the head waters of a reservoir.
- At position B, the particle has gained some speed at the expense of some potential energy illustrated by a small lowering of the free surface above B.
- At position C, more potential energy has been transformed into kinetic energy, as the particle follows fluid in a free fall trajectory.
- When the plunging flow comes into contact with water in the lower pool, vigorous momentum exchanges take place and a substantial part of the initial hydraulic energy has been lost to heat through the turbulent energy cascade and viscous processes.
- At position D, the particle leaves the domain with a lowered hydraulic energy compared with that of position A, B, and C.
While traveling from A to B and C, viscous and turbulent processes usually have little influence on the flow. Total hydraulic energy eG can be treated as a conserved quantity, like mass would be, with small loss terms taken into account if need be. Downstream of C, this model of conservative hydraulic energy can be extended by taking into account energy loss terms of a larger magnitude and effect on the flow.
Mass and Energy Budgets
Control Volumes
Both the transport of eG and mass density ρ have to be monitored for reasons that will become clear later on; this is simply taken for granted now.
The transport of eG and mass density ρ by the flow are easy to analyze with the help of control volumes, denoted as CV below, and Gauss’s law of divergence.
CVs are volumes enclosed by a defining surface of one choice as long as it follows these rules:
- The defining surface can be of arbitrary shape, as long as it doesn’t cross over itself.
- The surface may consist of patches, as long as each patch is connected to the others by watertight edges.
The volume of a CV is used to calculate integral, self-preserving quantities such as enclosed mass or energy.
The surface of a CV is used to define fluxes coming in and out, allowing one to make budgets of the enclosed quantities and to monitor their time history.
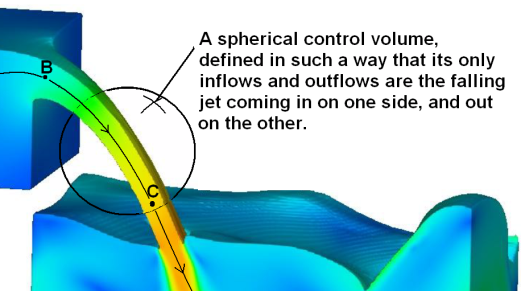
Figure 3 gives an example of a control volume that could be used to analyze the properties of a falling jet of water. The sole inflows and outflows into this control volume are the jet itself, coming in from the upper left and leaving at the lower right.
Control Volumes of Fixed Shapes in FLOW-3D HYDRO
With FLOW-3D HYDRO, CVs of fixed shape and position can be defined easily with the help of flux baffles of three basic shapes:
- Spheres, which are closed surfaces.
- Cylinders, which are open at both ends; because of their open ends, care must be taken to make them extend outside of the flow limits so that their ends do not have flow through them.
- Planar rectangular patches, which can be used to assemble a CV by having them cross an entire flow domain or subdomain.
Figure 4 is an example drawn from an actual model, where one can see the three types of flux baffles, after they have been rendered into a computational mesh. They are rendered as opaque but they are completely permeable to the flow if they are defined as solely flux measuring baffles.
(2) $latex \displaystyle {{h}_{G}}~\equiv ~{{e}_{G}}/\text{ }-g\text{ }\rho$
(3) $latex \displaystyle {{h}_{G}}\ =\quad z\ \ +\frac{p}{{-g\rho }}\ \ +\frac{{\left( {{{u}^{2}}+{{v}^{2}}+{{w}^{2}}} \right)}}{{-2g}}$
Figure 5 shows how to use planar baffle surfaces to define two control volumes:
- Control volume DC, an elongated cubic shape consists of six sides. Two opposite sides are the baffles called C and D; a bottom and a top side have been drawn and their position is inconsequential as long as they are well above and under the flow domain; a front and a back face are the two remaining faces of the cube and their position is also inconsequential as long as they are well in front and well at the back of the flow domain.
- Control volume BA is defined likewise. It encloses a part of the entrance portal, which is a sub domain that contains free surface flow. Free surface flows are more difficult to bring to a true steady state because differences in inflows on faces B and A impart a rate of change to the water level (and water volume) and result in oscillations that attenuate slowly or not at all. In these cases, reliable budgets of mass and energy are done by processing the time series of the flows in order to identify episodes where the properties’ evolution is stationary and perform averaging.
The vertical flux baffles in Figure 5 could be used to define several other CVs using permutations of the available vertical surfaces: DB, DA, CB, CA.
Energy Budget
The hydraulic energy balance is leaky by definition because it explicitly labels viscous heat production as a loss. Ideally, the hydraulic energy cascade should lose energy to no other cause, and should not gain any. Here again, practice with numerical models paints a slightly different picture. Any numerical model will have some artificial source or sink of hydraulic energy.
For instance, there is a flow interference with the computational mesh when the cell size is not much smaller than energy carrying flow features. When the cell size is not small enough, velocity contrasts are spread over larger spatial extents than in the natural flow. The spread makes the kinetic energy slightly smaller and acts as an energy dissipation that is due to grid effects rather than to natural phenomena.
Monitoring the energy budget may yield clues about the reliability of the model and can be used to compare runs that use different parameter values or grid cell sizes. When artificial gains and losses are under control, the rate of hydraulic energy dissipation is often one of the important results taken from numerical models and important for discriminating for between design variations.
Total Hydraulic Head
Total Hydraulic Head as an Energy Density
Total hydraulic head, symbolized as hG below, is the total hydraulic energy eG of Eq. 1 recast into an altitude by simply dividing it by (-g ρ ):
(2) $latex \displaystyle {{h}_{G}}~\equiv ~{{e}_{G}}/\text{ }-g\text{ }\rho$
(3) $latex \displaystyle {{h}_{G}}\ =\quad z\ \ +\frac{p}{{-g\rho }}\ \ +\frac{{\left( {{{u}^{2}}+{{v}^{2}}+{{w}^{2}}} \right)}}{{-2g}}$
where the symbols have all been introduced already except for:
hG, which is total hydraulic head (m)
Total hydraulic head is qualified as total because it is the sum of:
- piezometric head z + p/(-gρ)
- kinetic energy head u²/(-2g)
The piezometric head measured in the flow is considered to provide a good measurement of the water’s local free surface elevation.
In reservoirs and tranquil reaches of rivers, the flow’s velocity may be low enough that the kinetic energy head is considered negligible so that hG is sometimes taken to be equal to the piezometric head.
Total hydraulic head hG is sometimes called the stagnation height: given a particle of fluid within a flow, it is the ultimate height the particle would reach if all its velocity was suddenly directed upwards and the surrounding fluid was not an obstacle.
Total hydraulic head hG is an ubiquitous variable in hydraulic design, such as at bridge piers and abutments. It also stands in for the flow’s hydraulic energy whenever that energy has to be conveyed or dissipated in a managed fashion, such as along in channels and penstocks. hG is a variable of choice because it can appear in engineering drawings as annotations using the same altitude scales as other engineering work’s key heights.
Hydraulic Energy Dissipation from Integral Values of Total Hydraulic Head
The integral approach to energy dissipation occurring between two flow cross-sections A and B is calculated from the decrease in HG in the downward direction of the flow going.
To calculate the energy dissipation between A and B with the help of HG, the value of HGat each cross section is first multiplied by –ρg to cast it into an energy density flow, and then multiplied by Q to cast it into a total hydraulic energy flow.
Taking the difference in energy flows of two cross-sections, in a situation where the volume flow rate Q is the same at both cross-sections, yields the hydraulic energy loss incurred by the flow in moving from the upstream cross-section to the downstream one, as expressed below:
(4) $latex \displaystyle P\text{ }=\text{ }-\rho gQ\text{ }({{H}_{{GA\text{ }-}}}{{H}_{{GB\text{ })}}}$
where the newly introduced symbols have the following meanings:
Example 1 – A River Diversion
Figures 6 and 7 illustrate a river diversion through a tunnel. Only the water is shown. A river diversion is used on dam construction sites so that the dam’s foundations can be easily accessed and constructed.
In the example, water flows from left to right. The river is in a state of flood and it is flowing into the upper reach at a high rate. At times when the rate of incoming water is higher than the rate of outflow through the diversion, water accumulates in the upstream reach, the water level rises. The rise in water level increases the pressure on water in the tunnel, which increases the rate of flow in the tunnel, which decreases the rate of accumulation in the upstream reach. This negative feedback eventually equalizes and the rates of inflow and outflow stabilizes. The water level that is reached at peak flood is of much concern for managing the construction site.
The upstream reach presents an example of a volume balance where the water level fluctuates according to the difference between the incoming and outgoing flows. At the same time, the rate of flow through the tunnel results from a pressure balance between the upstream and downstream ends in which friction on the tunnel walls and flow energy losses at discrete structures and transitions along the passages play a large part. Figure 10 shows numerous flow measuring cross sections, known as flux baffles in FLOW-3D HYDRO. Their uses are many:
- Assaying the steadiness of the flow regime of any given model run, as a useful basis for further analyses
- Graphing and analyzing the longitudinal profiles water level, and hydraulic energy flow for many purposes, including hydraulic energy dissipation rates
- Allowing fine comparisons between design variations
- Verifying in general that the flow behavior conforms to expectations, detecting and correcting numerical artifacts that might reduce the flow’s verisimilitude if unchecked.
Example 2 – High Velocity Free Run Over a Natural Rock Surface
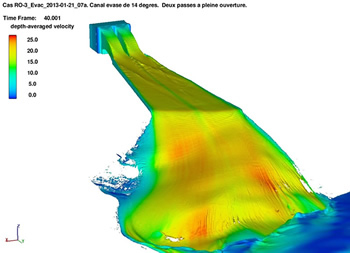
Figure 8 shows an example of a spillway’s tailrace and free run over natural rock.
The model was aimed at evaluating the rate of hydraulic energy dissipation per unit area of ground surface. This rate, in W/m², was an input for evaluations of the erosion potential of the rock surface along the free run.
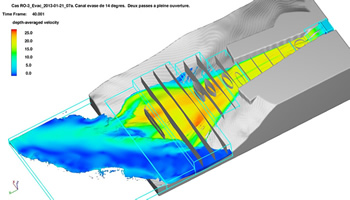
Figure 9 presents the metering apparatus that was used to ascertain the tools themselves and to perform the evaluations of the dissipation rate. The mesh blocks are also outlined.
An assortment of planar and cylindrical flux baffles were deployed for measuring the desired rate of dissipation and, just as importantly, for assessing the quality of the flow and measuring tools.
The planar flux baffles allow one to construct control volumes and use them to monitor the steadiness of the volume flow and the dissipation of energy within the CV. In the tailrace, the flow is well contained by sidewalls and fairly uniform across the cross-sections. The energy dissipation rates were of the order of 25 to 50 kW/m².
A cylindrical flow baffle is located at the foot of the discharge gates. The mean volume flow rate through the cylinder was variable through time because of normal flow fluctuations, but it did tend to zero when a suitable averaging interval was taken. When the same average was taken for the net hydraulic energy flow through the baffle, it yielded as expected a negative value which, divided by the area, was close to 30 kW/m². Another cylindrical flow baffle, extended into an elliptical horizontal cross-section, was also located near the end of the tail race. Similar verifications made there also showed a similar agreement.
It was concluded that the cylindrical flow baffles worked as expected for measuring hydraulic energy dissipation. Attention was then turned to the cylindrical baffles placed in the downward slope, where the dissipation was expected to be the highest.
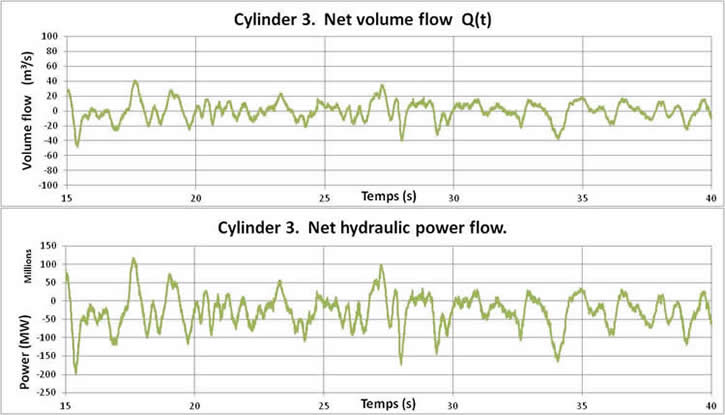
Figure 10 shows the time series of the net volume and energy flows through cylindrical baffle number 3, located over the free run, near the transition from the tailrace to the natural rock surface. The figure shows that high amplitude fluctuations of both flows are present and any tendency is rather well hidden by them.
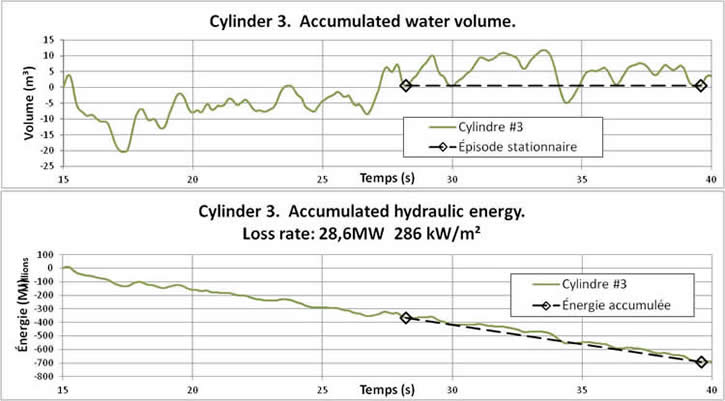
Figure 11 presents the time integration of the net volume and energy fluxes of Figure 10. The time integration yields values of volume (m³) and energy (J). The volume time series allows one to select a time interval where the regime is stationary, and to choose integration time boundaries so that the net volume change is close to zero. The energy time series shows a regular downwards trend, as expected for energy dissipation. The slope of the trend, in W/s, gives an estimate of the rate of dissipation. One can then divide it by the surface area of the base of the cylindrical baffle enclosure to get the desired dissipation rate per unit of area. The radii of the cylinder were chosen so that the area would be close to 100 m². In this case, the rate of dissipation found was 286 kW/m².
These results were then used in the discussions with engineers from other disciplines. It was made clear that the margin of uncertainty was large since, among other factors, the flow computation was not aerated ant the rock surface resulted from preliminary estimations. It was also pointed out by the modeller that hydraulic energy dissipates in the water, not in the rock, and that the location of maximum dissipation is not necessarily that of maximum action on the rock. The minutia of the analysis presented above was a significant burden but was deemed necessary as the baffles were being used in a way that was novel for the modeller. The cross-disciplinary discussions and the order of magnitude of the values were the most useful results of the model, rather than the numerical values themselves.
Conclusion
FLOW-3D HYDRO‘s flux baffles offer precise evaluations of volume and hydraulic energy net flows through them. Their computation algorithm is finely adjusted to the underlying numerical scheme of FLOW-3D HYDRO used with the control volume approach, they are well designed for numerous assays including verifying the performance of FLOW-3D HYDRO itself with regards to mass conservation in situations demanding a high level of consistency.
The computation of total hydraulic head can be made in numerous ways, a situation that is not surprising in view of the very high usefulness of the quantity to civil and hydraulics engineers. One of the ways offered by FLOW-3D HYDRO is the calculation over the flow area of a baffle of the flux averaged total hydraulic head. It is shown here that hydraulic energy rates of loss in a flow measured with the differences between the values at two flux baffles crossing a given flow tube will be exactly those that can be calculated with a control volume approach linked to primitive flow variables by the Gauss divergence theorem.