Why do we use Computational Fluid Dynamics (CFD)? The basic reason is that computer simulations can do things that experiments and mathematical analysis cannot. Once validated as a source of decent approximations of physical observations, a numerical simulation program can provide detailed information about a fluid flow problem, such as densities, pressures, temperatures and velocities throughout a flow. Initial and boundary conditions can be easily modified, and the consequences readily evaluated. These are the obvious things that make CFD useful. But there are more fundamental reasons for using CFD. In the following paragraphs, examples are used to show why CFD is fundamentally important. This presentation is only focused on fluid dynamics, but some of the reasons for computational analysis of fluids also applies to other kinds of continuum dynamics.
Modeling fuel sloshing in spacecraft
In spacecraft containing liquid fuel tanks, the fuel can slosh, causing unwanted forces that can interfere with the motion of the craft, as well as making the fuel difficult to access for powering the control jets. This sloshing in space, where there is little or no gravity, is a situation that cannot be duplicated with experiments on earth. In a computational simulation however, the magnitude of gravity can be set to any value, including zero. This, then is a situation where there is little or no alternative for studying the dynamics of liquid fuels in space craft. A good example of this is illustrated in the 2017 FLOW-3D User Conference presentation, “Modelling of upper stage dynamics including fuel sloshing,” by Francesco De Rose at Airbus Safran Launchers.
Liquid behavior in inkjet printers
A somewhat different problem will be familiar to most of us. Your computer may have a printer connected to it. Most often that printer uses inkjet technology, in which tiny jets of liquid ink are shot at a sheet of paper. These jets have a very small diameter (typically less than 60µm) and are designed to break up into tiny drops that are directed to form a pattern on paper. In many cases there may be multiple jets operating to speed up the printing process. Creating jets can be done in several ways using pressure pulses, moving diaphragms, pistons, etc. Once ink has been ejected from a nozzle, the chamber containing the ink must be quickly refilled so that another jet can be generated.

Because of their small size, and the short time of existence of an inkjet, it is difficult to observe the liquid behavior of pinch off and breakup of the jets. Furthermore, the fluid dynamics inside the mechanism that generates the jet cannot be observed in laboratory experiments. Instead, computational simulations can reveal the workings of inkjets in considerable detail, making the development of faster and more accurate printing possible. A great example of this application is provided by Kodak. Researchers at Kodak used FLOW-3D to simulate a new printhead design (Fig.1), for a pigment-based ink. CFD simulation allowed them to shave years off the design testing phase and bring a new product to market in a fraction of the time it would normally take.
There are many examples of inkjet type devices that benefit from CFD simulations. For example, Fig.2a shows a bubble generated at the junction of two optical channels. The bubble is intended to act like a switch that changes the direction of a light beam from straight through a junction to right angles into another channel. Researchers were initially not able to make this switch work and were unable to introduce sensing instruments because of its small size. A CFD simulation showed that liquid being evaporated at the bottom of the horizontal channel was condensing on the sides of the vertical channel, causing additional light reflections that prevented a clean switch operation (Fig.2b). Once seeing the problem, a fix was easily introduced that resulted in a smooth change in the light beam direction without having to introduce mechanical means.
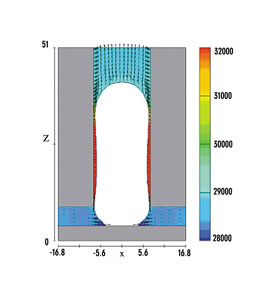

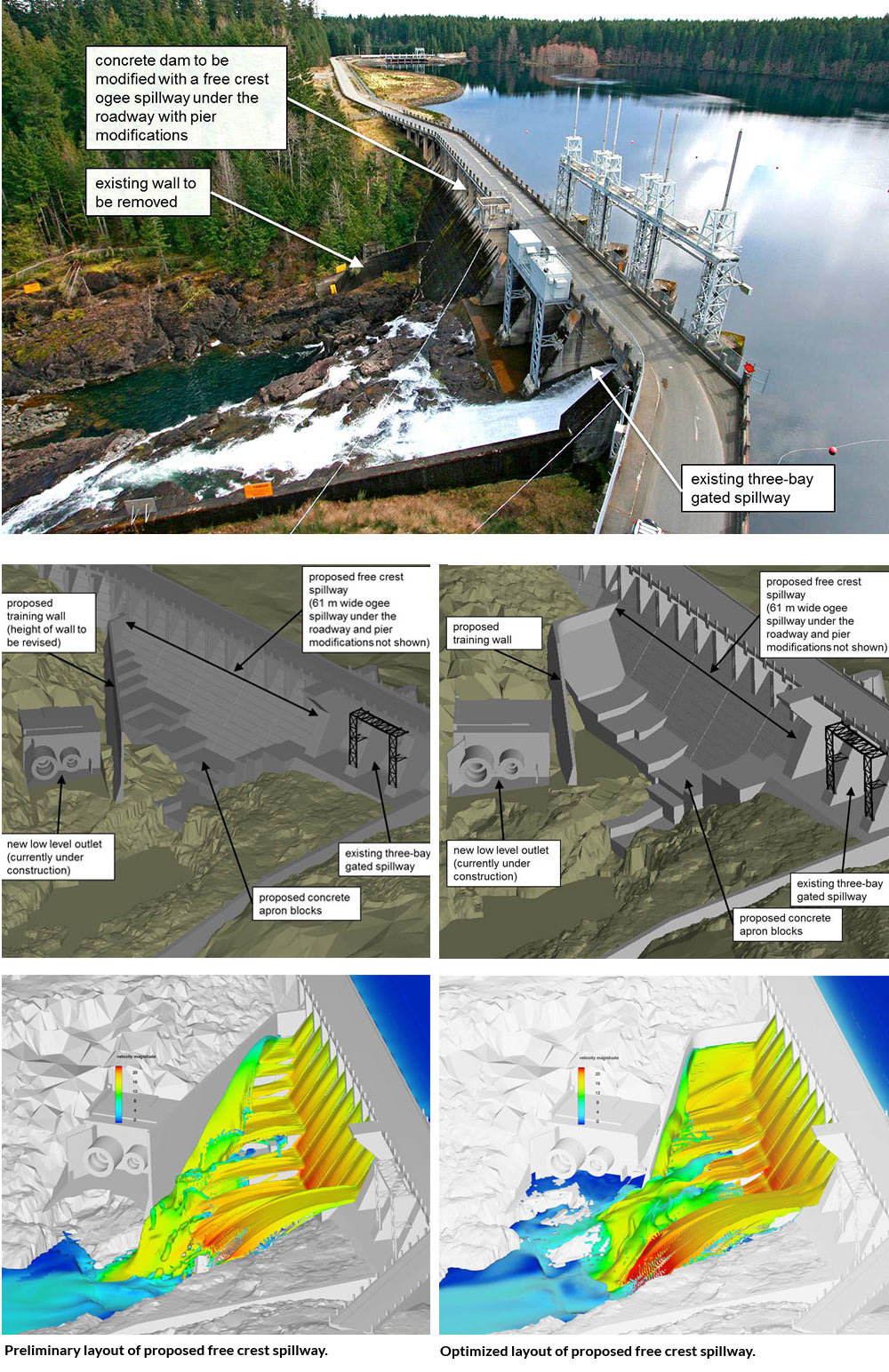
Large-scale hydropower projects
Another example involves large hydropower projects (dams and power stations), which are difficult to model in laboratory experiments, not only because of the expense, but because it is not possible to scale down the size of large installations without violating some scaling parameters that may change the results in unknown ways. A simple example of this would be a small-scale flume used to study wave propagation through or around various obstacles. At small sizes, surface tension may affect wave heights and wave speeds, while at larger scales surface tension is generally not important. Computational simulations have the flexibility to use any values for physical properties, so are not affected by scaling that would otherwise require a use of materials that may not exist.
The expense issue is, of course, very important. Large hydro projects can cost hundreds of millions of dollars and any errors in design can be catastrophic and are very expensive to correct. Furthermore, large projects involve many diverse types of flow situations that may influence one another.
Consider a hydroelectric power dam. There are intakes that require deflectors for fish or objects that could damage power generators. On the downstream side there is a spillway, the design of which must consider air entrainment which may affect the downstream ecology and cause possible scour damage at the base of the spillway. In case of a large rise in the upstream flow level, allowance must be made for overflow devices to relieve excess water without damaging the dam. Such considerations are why elaborate laboratory models are constructed to model these features. Their construction, however, is time consuming and expensive. And, just as in computational modeling, validation studies are needed to determine their accuracy.
In contrast, computational modeling can easily deal with large scales in which there are diverse flows. When necessary, computational models can be localized to study individual flow features in more detail. This flexibility is a definite advantage over physical models. Setting up a computational model is also much faster and less expensive than constructing a physical model
In the dam example shown in Fig. 3, several alternative designs of a proposed spillway were investigated using CFD simulations that could be quickly and inexpensively set up. Once the best design was selected, a physical model was constructed and used to confirm the CFD results.
An added advantage of using CFD in cases like this is that because it has been validated with the physical model, and while the physical model has been torn down to make room for other projects, future alterations to the dam can now be more quickly and less expensively investigated with confidence using additional computations.
Solving novel problems with CFD
The above examples provide reasons for why we use CFD. It must also be mentioned, of course, that CFD does have its limitations. For example, in the large hydro project’s discussion, involving a diverse set of flow issues, it may not be possible to computationally model all the flow features in sufficient detail because of a limitation in computer memory and/or computational cost. Should this be the case then the best solution may be to break up the simulation into manageable parts. The rapid growth in parallel and cloud computing resources is reducing this kind of limitation, but it will continue to exist as long as there are demands for more detail and a reduction in computational cost.
So why CFD? The answer is because it offers solutions to problems that may not be studied as closely, as thoroughly, or indeed in any other way.


