In this last blog on FLOW-3D CAST developments, I discuss the new Die Spray Cooling Model for thermal die cycling simulations.
In order to accurately predict the temperature distribution in the die in thermal die cycling simulations, the spatial variation in the spray cooling needs to be modeled. The Die Spray Cooling Model was developed for this purpose, and is now available in the recent release of FLOW-3D CAST. This model explicitly computes the cooling from each spray, instead of assuming a constant heat transfer coefficient across the entire die cavity. The spray area on the die surface is computed and updated constantly due to the movement of the spray nozzles. The model also takes into account the blocking of the fluid being sprayed, and thus the effect on cooling, due to the spray angle and the shape of the die surface. The new model provides accurate temperature distribution on the die surfaces with reliable and realistic input parameters, which helps engineers to better design and optimize the cooling process to eliminate hot spots. A sample thermal die cycling simulation demonstrates the capability of the new model, and the importance of explicitly simulating the die spraying process.
This simulation is based on the production of a vehicle structural part with large dimension and thin wall thickness. For this example, the simulation is limited only on the ejector part of the die. The two animations show the spray area on the die surface during spray cooling and the die surface temperature at the fifth cycle of spray cooling. The effect of global spraying and hot spot spraying can be clearly seen and identified.
Spray Area Computation
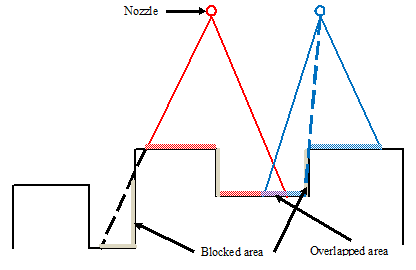
The influence of the shape of the die surface and the position of the spraying nozzles on the spray cooling is taken into account in the new model. As shown in the figure below, some areas under the spray on the die surface are blocked, and some areas are overlapped by two or more sprays. These areas are computed and identified using a ray tracing algorithm to distinguish the different spray cooling effects. The spray area can be visualized in FlowSight, along with other properties, such as the total spray time and total heat removed per unit area by the spray cooling.
Determining Heat Transfer Coefficients
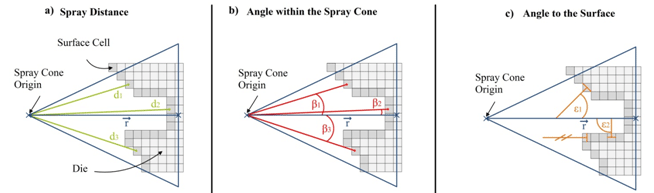
Spray cooling mechanisms are complicated, and the spray cooling heat transfer coefficient (HTC) depends on many variables such as spray shape, coolant flow rate, spray pressure, mold temperature, spray angles, and spray distance. To simplify the spray cooling HTC calculation, for every spray surface element, the HTC is computed by multiplying the base HTC by dependence factors, for example for a conical spray,
$latex \displaystyle HTC=HT{{C}_{0}}(T)\cdot {{f}_{d}}(d)\cdot {{f}_{b}}(\beta )\cdot {{f}_{e}}(\varepsilon )$, where
- HTC0 is the base spray heat transfer coefficient when the nozzle sprays on the mold from a specified distance. The base heat transfer coefficient is dependent on the spray cone characteristics, spray medium, and spray pressure, etc., and is a function of the mold surface temperature.
- fd is the distance d dependent factor function.
- fb is the spray angle β dependent factor function.
- fe is the spray angle (between the surface normal and the spray direction) ε dependent factor function
The meaning of the spray distance d, and spray angles β and ε are shown in the picture below.
The base heat transfer coefficient and the dependence factor functions can be curve fitted from experimental measurements, derived from theory, or from experience. If the sprays are not conical in shape, the dependence factors could be different.
About Nozzles
All spray nozzle groups are virtually mounted on the same robot arm. The translational and rotational movement of the robot arm can be specified in FLOW-3D CAST. If the motion data is saved in an external file, it can be imported from or linked to an external file. The capability of importing or linking external files significantly simplifies the input because the control data programmed for the spraying machine can be directly used for the model.
Nozzle properties can be directly read in from nozzle database. Since the heat transfer coefficient functions are dependent on the spray cone characteristics, including the spray cone angle, they are all part of the nozzle properties included in the nozzle database. If nozzle is not defined in the database, its properties can be directly input. The heat transfer coefficient functions can be constants or can be defined as tables. Similar to other table inputs, the data can be linked to external files. If the same nozzle is used often, its properties can be easily added to the nozzle database, similar to adding new material in the material database.
For each nozzle, the spray origin and end coordinates, or spray directions need to be defined. If the nozzle locations are pre-designed and the data is available, or the number of nozzles is relatively large, they can be read in from external files. If the number of nozzles is less the locations can be picked interactively and typed in a tabular form.
FLOW-3D CAST Wrap-Up
Following the design principle of WYSIWYN, FLOW-3D CAST introduced a process-oriented workspace for high pressure die casting. Users are now guided through the distinct stages of a high pressure die casting process – thermal die cycling, filling, solidification, and cooling. The new die spray cooling model, developed in collaboration with Audi AG, gives FLOW-3D CAST users the ability to model all facets of die preparation, taking into account the influence of the shape of the mold surface and the position and the movement of the spray nozzles. With these new features, metal casting engineers would be well-advised to give FLOW-3D CAST a try for efficient, accurate computations and increased productivity.
Learn about the latest developments in FLOW-3D CAST