Simulation of Joule heating-based Core Drying
This article was contributed by Eric Riedel 1,2
1Otto-von-Guericke-University Magdeburg, Institute of Manufacturing Technology and Quality Management, Germany
2Soplain GmbH, Germany
Modern casting production requires the use of sand cores. Growing environmental awareness as well as tougher regulations have supported the development of inorganic, emission-free binder systems, in which the cores are dried and cured by heat. In what is known as the hot box process, heat is generated in the core boxes and transferred to the sand binder mixture. However, the hot box process exhibits two major technological disadvantages.
The first disadvantage is the very low thermal conductivity of quartz sand of about 1 W/(m·K). Due to outside-in heat transfer, the process is time-consuming, can lead to shell formation and thus quality issues. For this reason, very high core-box temperatures of up to 523.15 K or more are applied to accelerate the heat transfer. The second disadvantage of the hot box process is that the core drying itself cannot be directly measured and digitized in real time. Instead, it can only be measured passively by recording peripheral parameters, such as from the core box.
The ACS Process
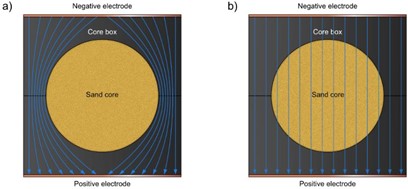
The new, patented Advanced Core Solution (ACS) process aims for time- and energy-efficient core drying and curing. The ACS process uses a property common to all inorganic binder systems: because they are water-based, they are electrically conductive. The key factor is the development of electrically conductive core box materials, whose conductivity can be adjusted to that of the sand-binder mixture. When a voltage is applied, the electrical current flows uniformly through the core box and sand-binder mixture, as demonstrated in Figure 1. Put more precisely, current flows through the electrically conductive binder bridges between the sand grains. Due to its inherent electrical resistance, the sand core heats uniformly without shell formation. The scientific principle behind it, called Joule heating, is based on Joule’s first law. In the series process, the electrically conductive core box heats up through Joule heating as well, additionally accelerating the drying process. This is a further important advantage, since for the ACS process, no complicated heating devices within the core boxes are required anymore, thus simplifying core box construction.
With this new process, and for the first time, heat is generated directly where it is needed: within the core. Since the necessary heat is generated through the homogeneously-distributed binder and transferred to the adjoining sand, the low thermal conductivity of the quartz sand is no longer a limiting process factor. Additionally, for the first time, the recording of drying-specific electrical parameters allows for comprehensive real-time monitoring of the drying process itself. Using FLOW-3D, the ACS process can be simulated, fulfilling an important criterion for industrial application, including the quantification of process benefits.
Model Description
The modeling is based on the work of Starobin et al. [1], but extends it with the Electro-mechanics model in FLOW-3D. Activating the electric potential (iepot = 1), takes electro-thermal effects, i.e., Joule heating (iethermo = 1), into account. Model details can be taken from [2]. Via the electrical properties of the components, the core box is assigned a dynamic potential (ioepotm = 1) with an electrical conductivity (oecond) and, if necessary, a dielectric potential (odiel); the same applies to the sand core in order to account for electrical conductivity of the entire sand-binder mixture. The electrodes are assigned a fixed potential (ioepotm = 0), an electrical conductivity, and a negative electric potential (oepot) for one electrode and a positive electric potential for the other. Since a temperature-dependent definition of the electrical conductivity is not yet possible, we worked with restart simulations and active simulation control. This way, the average electrical conductivities of the respective temperature ranges could be considered, i.e., 293.15 to 303.15 K, 303.15 to 313.15 K, and so on. The following investigations focus on one-fluid simulation, i.e., purging was not considered.
Example
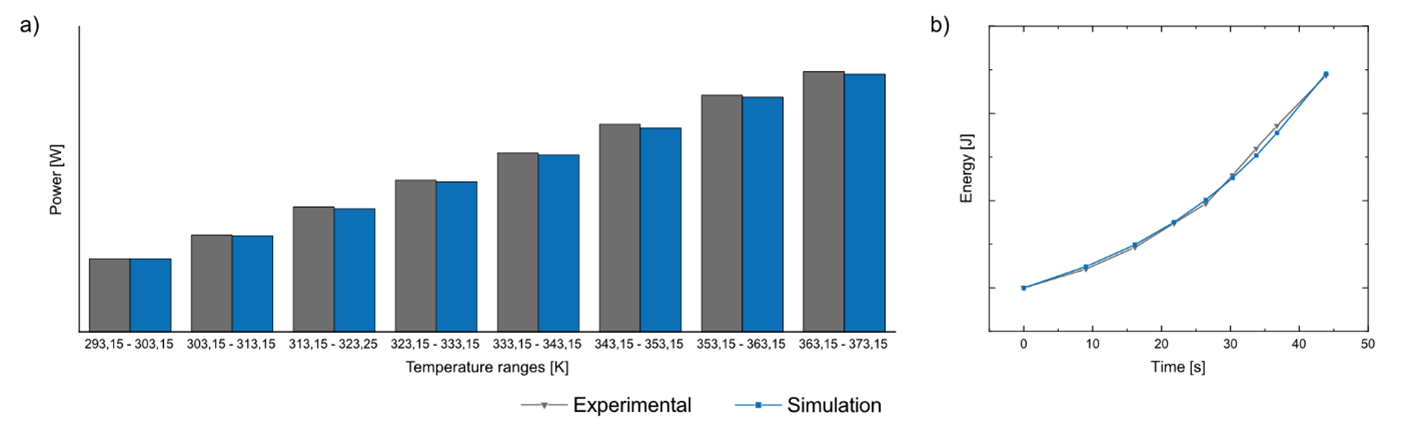
In the first step, a commercially available inorganic sand-binder mixture was used for the experimental investigation and validation of the simulation model to investigate heating and temperature-dependent electrical conductivity. The time required to reach 373.15 K as well as the power and energy input into the sand core were measured. Based on the experimental analysis and results, a basic simulation model was created. For reasons of discretion, some of the underlying results are presented only qualitatively. The results are demonstrated in Figure 2, showing high accordance between the measured values and the simulation.
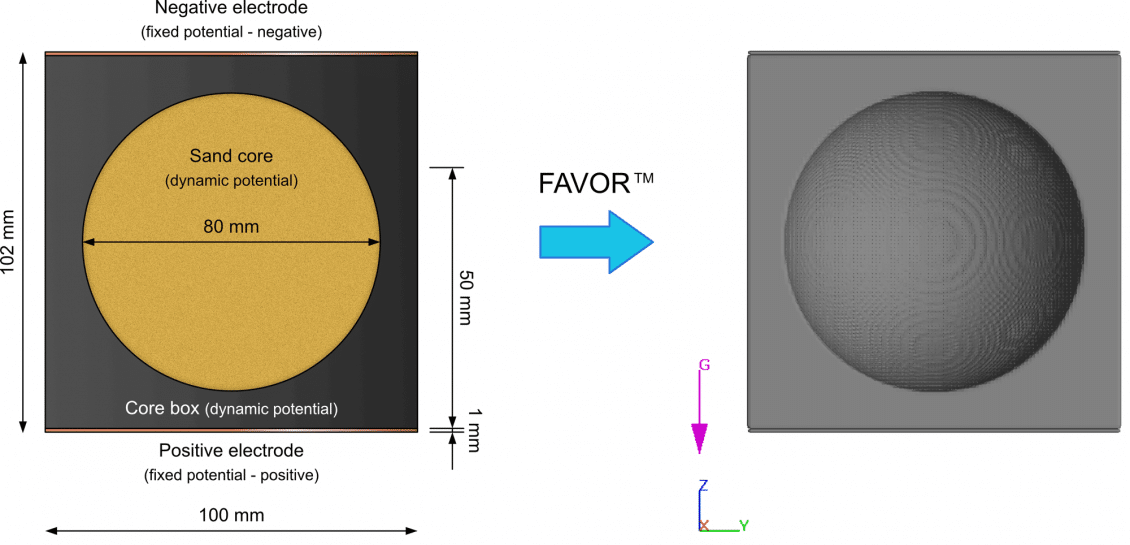
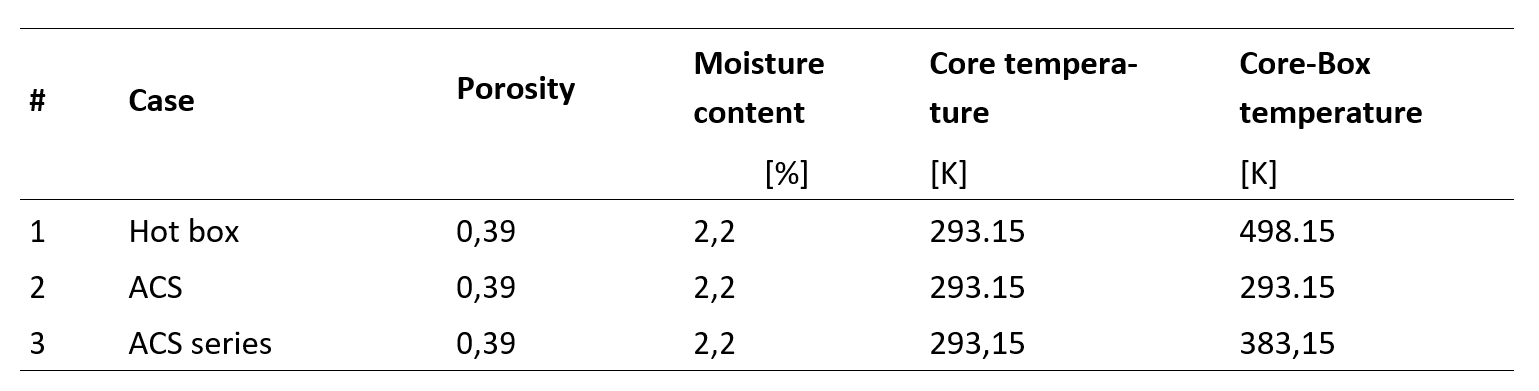
Based on the validated results, the ACS process and simulation are shown using a simple but high-volume geometry, which illustrates the fundamentals and high potential of the advanced ACS development compared to the classic hot box process. The geometric alignment can be taken from Figure 3. Three cases were simulated: (1) a classic hot box process; (2) an ACS cold start process with cold tool (293.15 K); and (3) an ACS series process accounting for the tool heating due to the Joule effect. All three-dimensional models were discretized with a cell size of 1 mm. Table 1 sums up the most important details of the calculated scenarios.
Results and Discusssion
Figure 4 shows the temperature and moisture development for the classic hot box process, clearly showing the outside-in heat transfer and corresponding moisture reduction. The simulation was carried out for 120 s with moisture still present in the sand core center at the end of the simulation; in practice, cycle time targets force an early termination of the drying process with shell formation and residual moisture in the core center. However, the ACS cold start simulation (corresponding to the first shot when the core shooting machine is started up), which is shown in Figure 5, shows the basic principle of the new process: the uniform heating of the core leads to an inside-out moisture transport. Furthermore, the sand core heats up faster than the core box. In the series process, the core box also reaches temperatures greater than 373.15 K through Joule heating, resulting in a mixture of hot box and ACS processes which further accelerates the drying process. The results of the ACS series simulation are summarized in Figure 6. While the sand core is not fully cured even after 120 seconds in the hot box process, the ACS process allows the core to dry completely after 72 or 45 seconds. Despite the significantly lower core box temperature, the new process shows a significant acceleration in core drying and the great potential of the new approach. One major advantage is a massive reduction in cycle times, including the associated energy requirements and the corresponding CO2 emissions. The energy introduced into the sand core can be measured during the real process as well as predicted in advance using simulation, which is another great advantage in terms of process design and transparency. Additionally, the simulation clearly illustrates the geometry-independent homogeneous heating of the test specimen, which means that moisture is not trapped in the core center and shell formation is avoided. All in all, the new process enables a significant increase in efficiency of the process and the quality of the inorganically bound sand cores as well. The process diagrams of all three cases are summarized in Figure 7.
Summary and Outlook
The demonstrated modelling shows the capability of FLOW-3D to simulate the new core drying process accurately as well as the potential of the new process for more efficient core drying and curing compared to the conventional hot box process. Even if the new simulation setup is still in the development stage and needs more real-case experiments, it still allows for great insights in the drying behavior, with very good agreement with experimental measurements so far.
Presently, within the simulation, the electrical conductivity of the sand-binder mixture is generated via the quartz sand, which in reality is not electrically conductive but corresponds to the electrical conductivity of the real-measured sand-binder mixtures. This way, the electrical conductivity of the entire sand-binder mixture is accounted for in the simulation and seems to fit the experimental results. For more precise simulations, the possibility of saving a temperature-dependent electrical conductivity of the solid core (i.e. the sand-binder mixture) would be helpful in order to take the actual conductivity curve into account. Further steps will concentrate on two-fluid simulation models. Initial trials show the basic feasibility with good results.
Despite the steps still to be taken, it can be said that the ability to simulate the ACS process with FLOW-3D marks an important milestone in the holistic establishment of a Joule heating-based core drying process and shows the benefits of this process for inorganic sand core manufacturing.
References
- Starobin, C.W. Hirt, H. Lang, M. Todte, Core Drying Simulation and Validation, AFS Proceedings, Schaumburg, IL USA, 2011
- FLOW-3D from Flow Science, Inc., Santa Fe, NM, USA