Open surface microfluidic systems are becoming increasingly popular in the fields of biology, biotechnology, medicine, point-of-care (POC) and home care systems. The design of such systems usually involves fluid being transported by capillary forces. Capillarity can enhance fluid transport for small volumes of fluid and can provide a reliable alternative to micro-scale pumping mechanisms. Advantages of capillary systems include:
- Low cost due to easy and fast fabrication
- User friendliness due to the simplicity of their design
- Increased portability ensured by the capillary actuation of fluids
- Enhanced accessibility caused by the open-surface nature of their design
- Complete elimination of air bubbles guaranteed by the uniformly moving fluid front
For these reasons, open capillary systems are the preferred design option for various POC systems.
Condition for Onset of Capillary Flow
In a recent paper from researchers from the University at Buffalo and University of Grenoble, it was shown how microgrooves can potentially enhance the capillary effect [1]. Based on the results of this paper, I will discuss a case study of the spontaneous capillary flow (SCF) of fluids inside a narrow V- groove microchannel surmounted by parallel plates using FLOW-3D. Large fluid velocities can be obtained, even with viscous fluids such as whole blood for the design of POC systems to monitor blood flow, if certain conditions for the onset of capillary flow are satisfied.
The conditions of capillary flow can be theoretically established using a static approach based on the minimization of Gibbs free energy. More specifically, the condition for the onset of capillary flow with a zero inlet pressure is:
(Eq. 1) $latex \frac{{{{p}_{F}}}}{{{{p}_{W}}}}<\cos \theta $
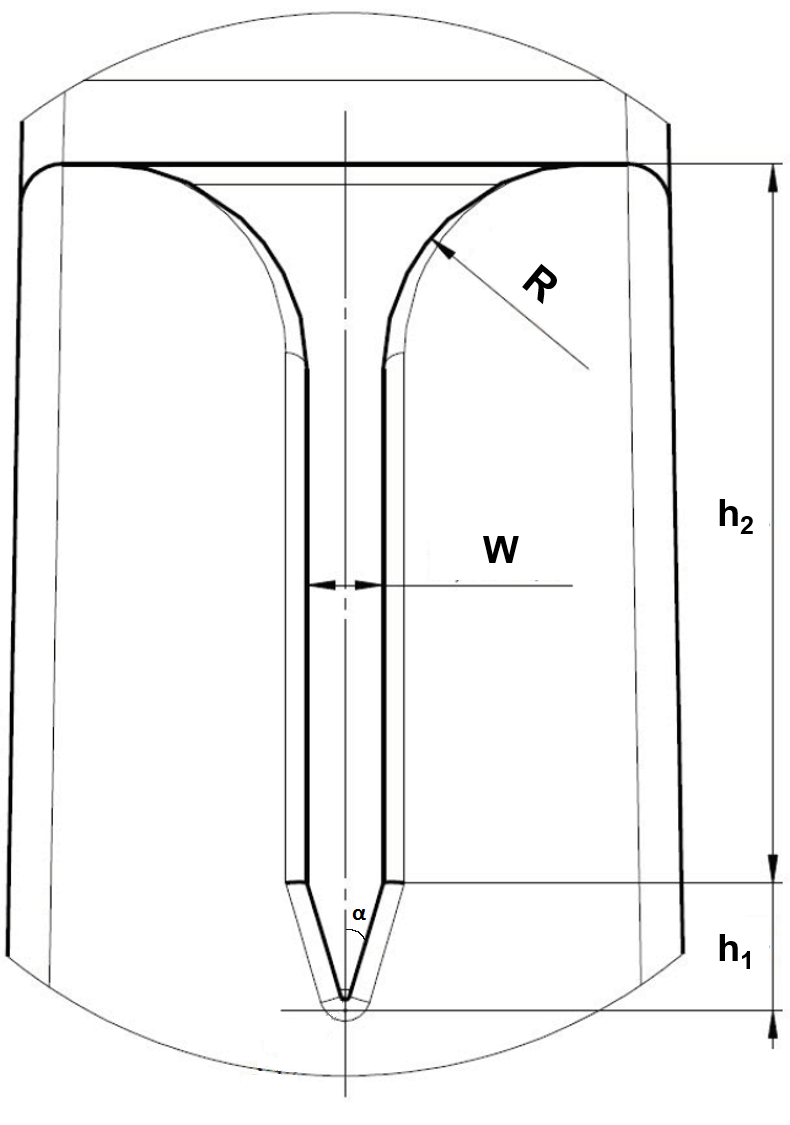
where θ is the Young contact angle, and pF and pW are the free and wetted perimeters, respectively, in an arbitrary cross section of the flow. For a V-groove microchannel with a half-angle α, such as the one shown in Fig. 1, after a few mathematical manipulations, eq. 1 can be rewritten as:
(Eq. 2) $latex \displaystyle \sin \alpha =~\cos \theta $
In our case we have α ≈ 14.5ο, hence the condition for capillary flow is θ < 75.5o.
Simulating in FLOW-3D
Although a static approach provides important information concerning the onset of SCF, a numerical approach is more appropriate for studying flow dynamics in a point-of-care device. A CFD analysis was performed for a V-groove microchannel with a contact angle of 37o and fluid properties of whole blood. Viscosity of blood is nearly constant, hence the flow regime is considered to be Newtonian [1]. A uniform ambient pressure was applied at all boundaries and throughout the computational domain to ensure that the fluid motion was caused only by capillary effects. The simulation was split into two parts: an initial simulation covering the first 4mm of fluid travel and a restart simulation to predict the fluid transport from 4mm to 8mm.
Results and Validations
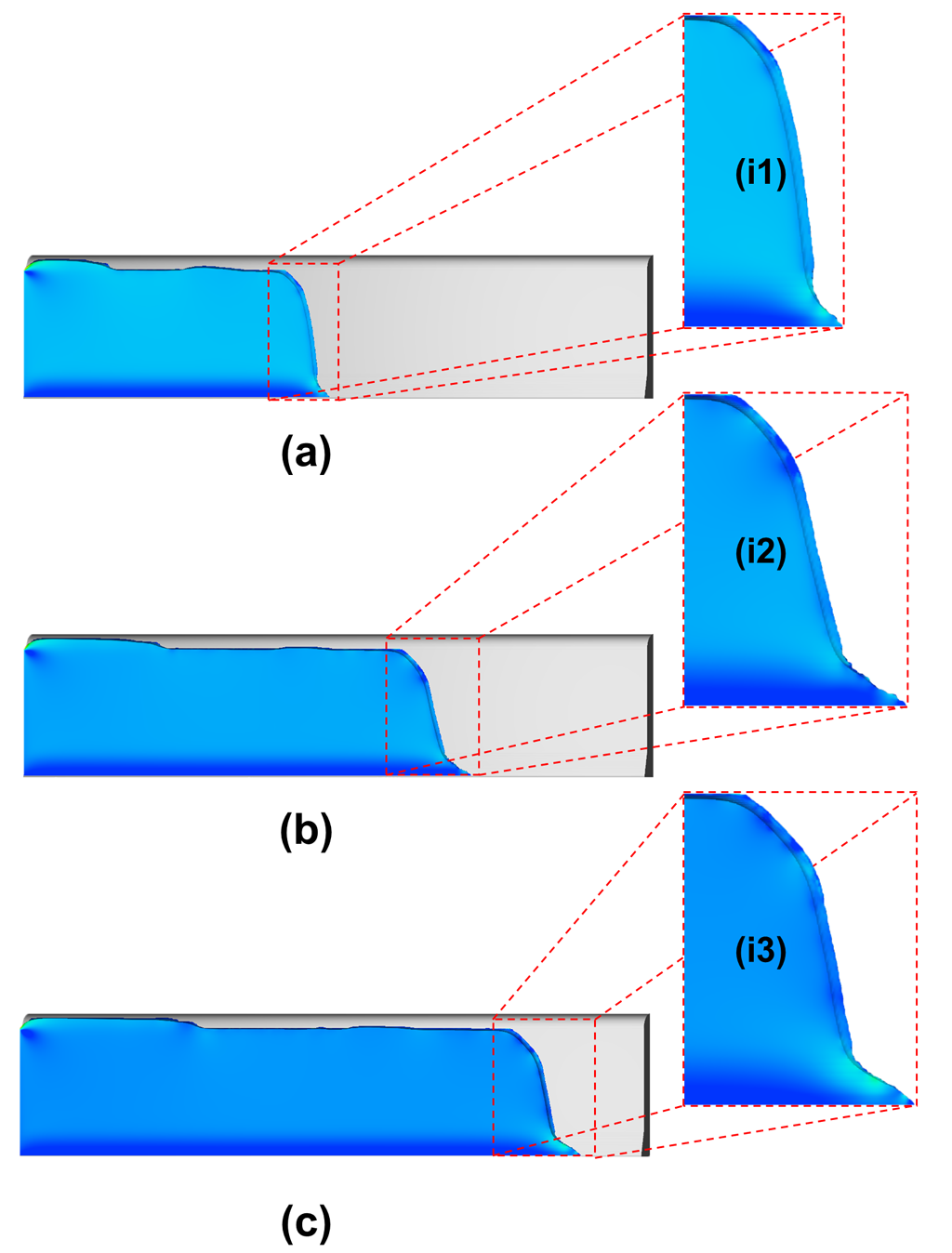
The flow dynamics for the first 8mm of travel are shown in Fig. 2. This figure shows the shape of the advancing interface in the slot at three different times. The progressive extension of the filament (Concus-Finn filament) can be seen ahead of the main flow.
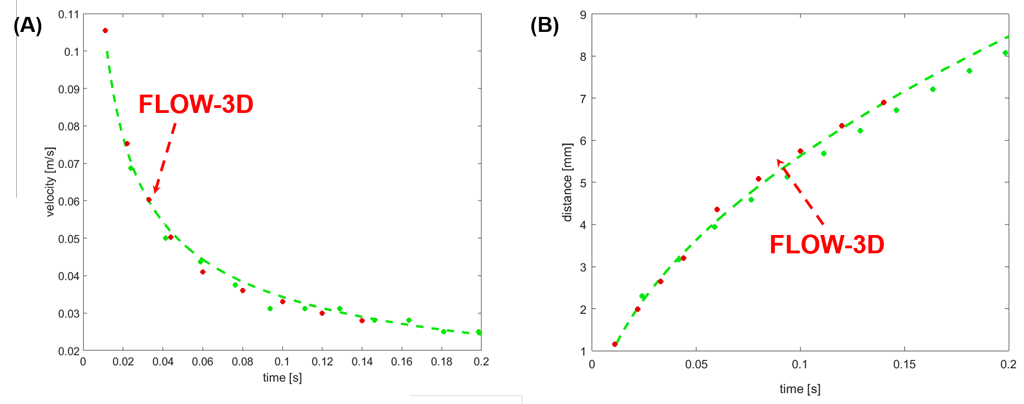
A comparison between analytical, numerical and experimental results is shown in Fig. 3. There is excellent agreement between numerical predictions and experiments. Although an analytical solution is also plotted, it may not represent a valid comparison, against numerical and experimental results, as the effects of the Concus – Finn filament at the bottom of the channel are not taken into account.
In addition to whole blood, different fluids were also studied in the experiment, including water tinted by food coloring and a viscous solution of alginate to test the potential of the device to move highly viscous fluids. Highly viscous fluid like blood could be moved within times less than 1s (see animation below).
The case study demonstrates that for whole blood, which has a relatively large viscosity (4 times that of water), velocities up to 7.5 cm/s were achieved. Based on experimental results and FLOW-3D predictions, the whole channel was filled with blood in less than 0.2 s. FLOW-3D simulation results are in excellent agreement with experimental observations, which also indicate that the velocities decrease with the distance inside the V-groove, but remain significant throughout the length of the device.
References
- Berthier, J., K. Brakke, E. P. Furlani, I. H. Karampelas, and G. Delapierre. “Open-surface microfluidics.” In Proceedings of the Nanotech International Conference, pp. 15-19. 2014.
- Hirt, Cyril W., and Billy D. Nichols. “Volume of fluid (VOF) method for the dynamics of free boundaries.” Journal of computational physics 39, no. 1 (1981): 201-225.
- Rajaratnam, N., and M. R. Chamani. “Energy loss at drops.” Journal of Hydraulic Research 33, no. 3 (1995): 373-384.