VOF – What’s in a Name?
In CFD, a free surface is an interface between a liquid and a gas in which the gas can only apply a pressure on the liquid. Free surfaces are generally excellent approximations when the ratio of liquid to gas densities is large, e.g., for water and air the ratio is 1000.
VOF Method Components
In FLOW-3D free surfaces are modeled with the Volume of Fluid (VOF) technique, which was first reported in Nichols and Hirt (1975), and more completely in Hirt and Nichols (1981). The VOF method consists of three ingredients: a scheme to locate the surface, an algorithm to track the surface as a sharp interface moving through a computational grid, and a means of applying boundary conditions at the surface.
Two-fluid VOF
When using the VOF method to model both liquid and gas, or two liquids, the interface between them does not require the setting of the boundary conditions. The VOF method in this case reduces to two or even one of the three original VOF ingredients. Users of such methods should be aware that two-fluid VOF schemes sometimes give incorrect results, especially when a single velocity field is used to capture the fluid mixture flow.
Two-fluid VOF methods use a fluid volume fraction to locate the interface, but they then attempt to compute flow in both the liquid and gas regions, instead of accounting for the gas by a boundary condition. This practice produces an incorrect motion of the surface since it is assumed to move with the average velocity of gas and liquid. In reality, the two fluids generally move independently of one another except for a thin viscous boundary layer.
One-fluid VOF vs. Two-fluid VOF Example
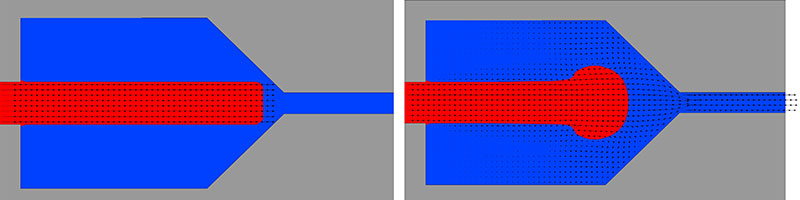
The consequences of trying to compute both gas and liquid flow can be illustrated with a simple example. All the computed results shown here were produced with FLOW-3D, which has a two-fluid option that is run in a VOF mode. Imagine a jet of water issuing at constant velocity from a long slit into air. If we neglect gravity and keep the velocity of the jet low (say 10.0 cm/s), we expect the jet to move more or less unimpeded by the air (see the FLOW-3D results in Fig. 1), obtained with its VOF free-surface model).
Two-fluid VOF methods produce a growth at the tip of the jet (Fig. 2). This growth is numerical, not physical, because it is independent of the density of air (e.g., the growth remains largely unchanged for air densities 100, 1000 and 10,000 times smaller than the liquid density).
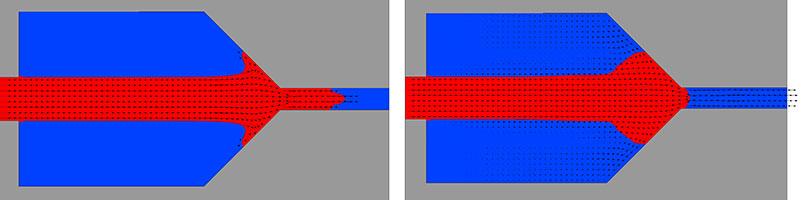
At later times the FLOW-3D jet (Fig. 3) strikes the right-hand wall and a small portion of the flow has entered a slot in the wall.
In contrast, the lower density air flow in the two-fluid VOF method is pulling liquid into the slot just before the jet strikes the wall (Fig. 4). Also, because of the incompressibility of the air remaining in the chamber, the amount of liquid flowing out the slot in the two-fluid VOF method must be equal to the amount injected, which is more than would be expected under most physical conditions.
A common approach to two-fluid VOF is to use some type of higher-order advection scheme to track interfaces, where the interface is represented as a rapid change in density. Such schemes result in smoothed transition regions between gas and liquid that cover several control volumes rather than sharp interfaces localized in
one control volume as is done in the one-fluid as well as the two-fluid VOF methods in FLOW-3D. In other words, the two-fluid VOF method in FLOW-3D retains two of the three component of the original VOF model, while still using a single velocity field for the mixture.
While on the face of it the one-fluid VOF method looks simpler because gas is not included in the flow, its numerical aspects are far from it. Implementing free-surface boundary conditions requires exceptionally accurate tracking of the interface and it must be done carefully to avoid numerical instabilities. Similarly, confining the fluid interface to a single control volume in the two-fluid VOF method in FLOW-3D is numerically challenging, as any such discontinuity in material properties can be a source of instabilities.
FLOW-3D has all the ingredients recommended for the successful treatment of free surfaces. Moreover, it incorporates major improvements beyond the original VOF method in each of its three major ingredients.
References
Nichols, B.D. and Hirt, C.W., “Methods for Calculating Multi-Dimensional, Transient Free Surface Flows Past Bodies,” Proc. First Intern. Conf. Num. Ship Hydrodynamics, Gaithersburg, ML, Oct. 20-23, 1975
Hirt, C.W. and Nichols, B.D., “Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries,” Journal of Computational Physics 39, 201, 1981.