In this article, Dr. Tony Hirt discusses the new Steady-State Accelerator, available in the upcoming release of FLOW-3D v12.0.
There is frequently a need to have a faster way to generate a steady free-surface flow than by simply trying to compute the asymptotic state of a transient flow. The situation is similar to solving for incompressible flow by trying to use a compressible flow solver. In the latter case, compression waves can take a long time to decay and leave a resultant incompressible flow. Correspondingly, in free-surface flows the fluid is incompressible, but surface waves may require a long time to damp out to produce a steady free-surface configuration.
In the incompressible flow case, we use an iterative process (i.e., the pressure-velocity iteration) that critically damps compression waves. Physically, the iteration allows pressure-like waves to travel short distances that influence localized regions, but that then damp quickly enough to avoid long range propagation and reflections that could introduce considerable noise in the pressure field.
In this note, a simple pressure adjustment applied to free-surface cells acts as a damping force on surface disturbances. This damping accelerates the approach to a steady free-surface configuration.
Steady-State Accelerator Idea
Fluid interfaces or free surfaces are tracked in FLOW-3D using the Volume-of-Fluid (VOF) technique. The fraction of fluid variable F locates the regions occupied by fluid. If a fluid has a stationary free surface the F values defining the fluid must also retain steady values. For F to be constant, the fluid velocity normal to the surface must be zero. Of course, the tangential fluid velocity at a surface does not have to be zero. For example, in flow over a weir there is constant flow but the location and shape of the stream off the step is unchanging.
To have a steady-state solver for free-surface flows, a way must be found to drive the normal surface velocity to zero while maintaining the incompressibility of the flow.
One way to accomplish this is to adjust the surface pressure in a way that will drive the normal velocity towards zero — in particular, to add a “damping” pressure contribution to the total surface pressure that is proportional to the normal velocity, being positive if the velocity is directed out of the surface and negative otherwise.
As a zero normal velocity is approached, the corrective pressure must also go to zero so that the surface is not likely to overshoot the stationary position. Of course, overshoots could happen if the correction is too large. For this reason, there must be some limiting factors for a stable application of the correction.
A coefficient acronym, ssacc, which stands for Steady-State Accelerator, has been added to the program input to activate this new option. The value for ssacc should be less than or equal to 1.0, a convenient upper bound. There are several limiters automatically applied to the damping pressure within the program to prevent it from introducing instability or adversely affecting transient phenomena.
The previous issues about stability and damping limiters deserve to be emphasized. When the steady-state accelerator is used, then all transients in a free-surface flow can no longer be viewed as completely realistic. The damping pressure is not physical force, but rather a mechanism to reduce wave propagation and reflection. The damper has been devised to not interfere with the evolution of large transients and should only contribute to a more rapid attainment of steady results as the flow settles down. Users should be alert, however, to possible excess damping that the limiters might not have anticipated, which can be eliminated by reducing the input value of the damping coefficient ssacc.
Two examples serve to illustrate how the steady-state accelerator’s damping mechanism works.
Steady-State Accelerator Examples
Collapse of Raised Fluid Column
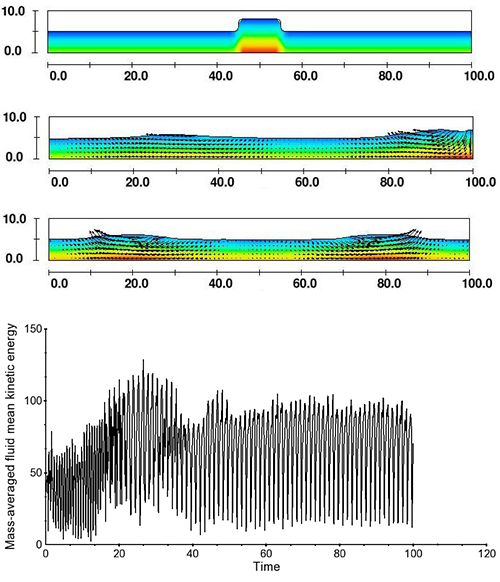
The first example consists of a two-dimensional pool of water 100cm long and 5cm deep. All boundaries of the tank containing the water are symmetry boundaries. At the center of the pool there is a block of water sitting on top of the pool that is 10cm wide and 3cm high. This block falls into the water because of gravity and generates waves that travel away from the point of impact and then reflect from the ends of the tank. After 100s there is still significant wave action because of repeated reflections (Fig.1).
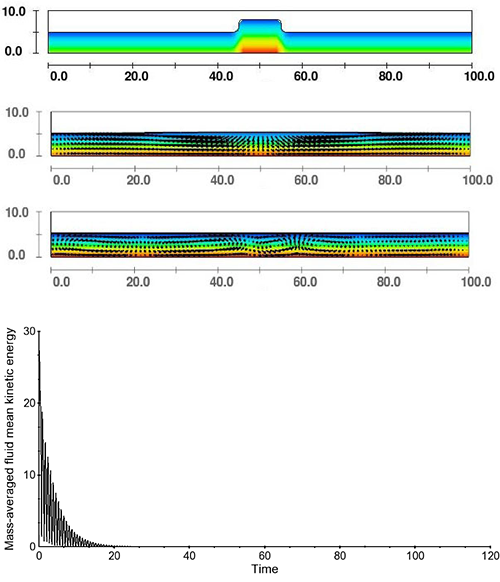
When the new steady-state accelerator is used with the coefficient ssacc=1.0 all the waves are quickly damped resulting in a nearly flat surface. Some residual flow remains under the surface, but this is slowly damping out under the action of viscosity (Fig. 2). In this example the added damping is particularly impressive.
Capillary Rise in a Square Channel at 45° in a Rectangular Grid
The capillary rise of fluid in a vertical channel is a good steady-state problem for which there is a simple analytical solution: the amount of fluid raised against gravity is determined by the wall adhesion — that is, the surface tension times the cosine of the contact angle times the length of the contact line. In this example the fluid is water, with a surface tension of 70 dynes/cm and contact angle of 30°. The channel is square in cross-section, having an edge length of 0.707cm and rotated by 45° in a rectangular grid. Only a quadrant of the grid is modeled as the problem has symmetry in the x and y directions. At the bottom of the grid there is water at zero gauge pressure and the grid has cubic elements with edge length of 0.0125cm (41x41x80 cells). The theoretical volume of fluid that should be raised is 0.04373cc. Figure 3a shows the steady-state result, which is similar whether damping is used or not. The fluid volume computed without damping is 1.74% higher than the theoretical value; it is 2.24% too high for the case with damping, as shown in Fig 3b. Note that when the accelerator is used, steady state is achieved at about 0.15s, while the standard solver produces a steady-state solution only after 0.8s, taking more than five times longer.

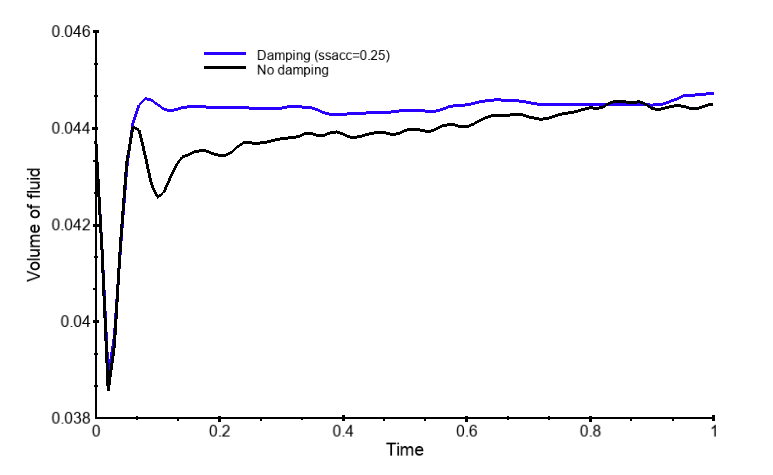
When ssacc is less than 1.0, convergence is reached sooner because of less damping, although all values of ssacc, including 1.0, result in converged solutions that are in close agreement with theory and exhibit fewer small bits of fluid on the back wall compared to the non-damped ssacc=0.0 case.
The small bits of fluid on the back wall originate from an overshoot of fluid above its equilibrium position, which then falls back leaving a small amount of fluid on the wall requiring a long time to settle down because of viscous forces. This overshoot is eliminated when ssacc is nonzero.
